Longest Substring Without Repeating Characters
Description
Given a string, find the length of the longest substring without repeating character.
example
Input: "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3.
solution
1. 方法一:暴力法
检查每一个子字符串是否有重复的字符1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length();
int ans = 0;
for (int i = 0; i < n; i++)
for (int j = i + 1; j <= n; j++)
if (allUnique(s, i, j)) ans = Math.max(ans, j - i);
return ans;
}
public boolean allUnique(String s, int start, int end) {
Set<Character> set = new HashSet<>();
for (int i = start; i < end; i++) {
Character ch = s.charAt(i);
if (set.contains(ch)) return false;
set.add(ch);
}
return true;
}
}
算法分析:
时间复杂度:O(n3);
空间复杂度:O(min(m,n))
2. 方法二:滑动窗口
滑动窗口经常用在数组和字符串的问题中,滑动窗口是数组和字符串中的一些元素,它用两个索引来表示滑动窗口的起始位置[i,j),滑动窗口通过滑动左右的两个索引来改变滑动窗口滑动的方向以及窗口内的元素.
本题用HashSet来存储现在的滑动窗口内的元素[i,j),通过检查第j个元素,如果不在集合中就存储到集合并继续增加滑动窗口右侧可值j,如果第j个元素已经在集合中了,那么就滑动左侧的索引i,从集合中删除第i个元素,直到此时第j个元素不在集合中了。
代码实现1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length();
Set<Character> set = new HashSet<>();
int ans = 0, i = 0, j = 0;
while (i < n && j < n) {
// try to extend the range [i, j]
if (!set.contains(s.charAt(j))){
set.add(s.charAt(j++));
ans = Math.max(ans, j - i);
}
else {
set.remove(s.charAt(i++));
}
}
return ans;
}
}
算法分析:时间复杂度:O(2n)=O(n)
3. 方法三:滑动窗口的优化
利用HashMap来代替HashSet1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public int lengthOfLongestSubstring(String s) {
int n=s.length();
int maxn=0;
Map<Character,Integer> map=new HashMap<>();
for(int i=0,j=0;j<n;j++){
if(map.contains(s.charAt(j))){
i=Math.max(map.get(s.charAt(j)),i);
}
amxn=Math.max(maxn,j-i+1);
map.put(s.charAt(j),j+1);
}
return maxn;
}
}
算法分析:时间复杂度O(n)
Longest Palindromic Substring
回文字符串:正读反读都一样
1.方法一:暴力法
遍历所有的子字符串,判断它是不是回文字符串
1 |
|
算法分析: 时间复杂度O(n^3)
2. 方法二:动态规划
暴力法时间复杂度高的原因是去检查每一个子字符串是不是回文的,降低时间复杂度就要减少对子字符串是不是回文的判断
假设一个字符串”ababa”,当我已经确认了”bab”是回文字符串,由于它左右两边的字符都是a,那么这个完整的字符串本身就是回文的,就可以不用对整个字符串再进行完整的判断。
假设一个字符串的长度为n,那么建立一个n*n数组P。在矩阵中P[i][j]=l,若l>0:表示以字符S[i]开始和以S[j]结尾的字符串是回文字符串,字符串的长度为l;若l=0,表示此字符串不是回文字符串
只需要对矩阵中j>=i的部分赋值即可,就j<i部分为0;
1.一个字符的情况:将矩阵的对角线赋值为1,因为每个字符本身是回文的
2.两个字符的情况:j-i=1
P[i][j]=2,if S[i]=S[j]
3.多个字符的情况:j-i>=2
if S[i]!=S[j]
P[i][j]=0;
if S[i]=S[j]
if P[i+1][j-1]>0
P[i][j]=p[i+1][j-1]+2;
else
P[i][j]=0;
字符串有多个字符组成时,如果两边的字符相等,那么这个字符串可能是回文的,这时将字符串去掉首末字符得到子字符串,如果子字符串回文的,那么这个字符串也是回文的。
1 |
|
算法分析:
时间复杂度:O(n^2)
空间复杂度:O(n^2)需要一个n*n的矩阵来存储数据
3.方法三:Expand Around Center
对于动态规划算法时间复杂度为O(n^2),空间复杂度为O(n^2),可以进一步优化只用O(1)的空间实现O(n^2)的时间复杂度
一个回文字符串它是成中心对称的,比如”baab”,”bab”,但是回文字符串分为两种:奇数字符数,偶数字符数
1 |
|
算法分析
时间复杂度:O(n^2)
空间复杂苏:O(1)
4.方法四:最长公共字符串
将字符串S翻转为S’,检查S和S’的最长公共字符串就是S的最长回文子字符串
此方法中存在一种问题,就是当字符串中某一个子串存在一个镜像子串本身并不是回文的,翻转之后会被检测为回文的。
Longest Common Substring 最长公共子字符串
动态规划问题
动态规划问题的两个特点:
1.最优子结构
2.重叠子问题
因为有重叠子问题,当前计算的过程中可能有的问题在之前的计算已经计算过了,现在又要计算一遍,导致大量重复的计算
动态规划通过找到解决问题的递推关系,将已经完成计算的存储起来,当开始新的计算时如果包含之前计算的子问题时,不需要再次计算,只需要访问已经存储的计算结果就可以
动态规划解决问题的方法一般减少了时间复杂度,增加了存储空间。
对于这个问题,假设有两个字符串s[0,…m],t[0,…,n],求两个字符串的最长公共子字符串
定义矩阵mXn的矩阵L,L[i][j]表示以s[i]开始和t[j]结尾的公共子字符串长度的最大值,那么对于L[i+1][j+1]只是比L[i][j]增加了s[i+1]和t[j+1]
因此可以构造出最长公共子字符串的递归式:
if s[i]==t[j]
L[i][j]=L[i-1][j-1]+1
if s[i]!=t[j]
L[i][j]=0
假设有两个字符串:”ABAB”和”BABA” ,构造出了上述的矩阵
代码实现1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public static String LCS(String s1,String s2){
if(s1.isEmpty() || s2.isEmpty()){
return "";
}
int indexMax=0,maxn=0;
int[][] L=new int[s1.length()][s2.length()];
for(int i=0;i<s1.length();i++){
for(int j=0;j<s2.length();j++){
if(s1.charAt(i)==s2.charAt(j)){
if(i==0 || j==0){
L[i][j]=1;
}else{
L[i][j]=L[i-1][j-1]+1;
}
}
if(L[i][j]>maxn){
maxn=L[i][j];
indexMax=i;
}
}
}
return s1.substring(indexMax+1-maxn, indexMax+1);
}
算法分析:
时间复杂度:O(m*n)
空间复杂度:O(m*n)
算法优化
从上面动态查找最长公共子字符串的过程中发现,在循环查找的过程中只会用到矩阵L中的两行,即正在计算的一行和完成计算的上一行,之前计算的和带计算的都用不到,所以只需要维护两行数据就足够了,不需要使用mxn的数组
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class LCS_improve {
public static String LCS_improve(String s1,String s2){
if(s1.isEmpty() || s2.isEmpty()){
return "";
}
int indexMax=0,maxn=0;
int [][] L=new int[2][s1.length()];
for(int i=0;i<s1.length();i++){
int cur=(i+2)%2;
int pre=(i+1)%2;
for(int j=0;j<s2.length();j++){
if(s1.charAt(i)==s2.charAt(j)){
if(i==0 || j==0){
L[cur][j]=1;
}else{
L[cur][j]=L[pre][j-1]+1;
}
}else{
L[cur][j]=0;
}
if(L[cur][j]>maxn){
maxn=L[cur][j];
indexMax=i;
}
}
}
return s1.substring(indexMax+1-maxn, indexMax+1);
}
}
算法分析
时间复杂度:O(mn)
空间复杂度:O(min(m,n))
Longest Common Prefix
Description
Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string “”
Example
Input: ["flower","flow","flight"]
Output: "fl"
Solution
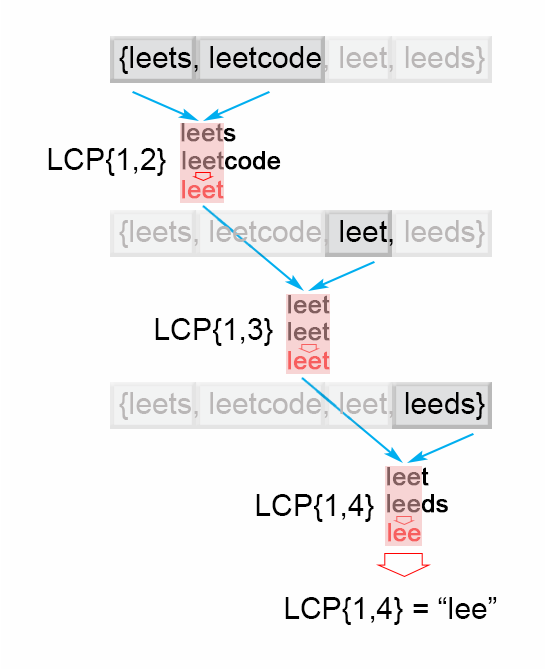
1. 方法一:横向比较
这是一种迭代的方法,假设字符串数组的长度为n,先将第一个字符串和第二个字符串比较得到最长公共前缀prefix,再将得到的prefix和第三个字符串比较得到新的prefix,依次向后比较,直到最后一个字符串。如果比较的过程中有prefix为空时,直接返回” “,LCP(S1,S2,.....,SN)=LCP(LCP(LCP(S1,S2),S3),.....SN)。
public String longestCommonPrefix(String[] strs) {
if (strs.length == 0) return "";
String prefix = strs[0];
for (int i = 1; i < strs.length; i++)
while (strs[i].indexOf(prefix) != 0) {
prefix = prefix.substring(0, prefix.length() - 1);
if (prefix.isEmpty()) return "";
}
return prefix;
}
算法分析
时间复杂度:在最坏的情况下为O(S),S为字符串数组中所有字符的总数
空间复杂度:O(1)
2. 方法二:纵向比较
横向比较需要从第一个字符串比较到最后一个,如果数组中最短的字符串再最后的位置,那么在整个算法执行的过程中会有很多不必要的比较运算,增加了时间复杂度。因此采用纵向的比较,以最短字符串的长度l为标准,最多只比较到每个字符串的l位。从所有字符串的第一个字符开始比较,对位比较所有的字符串,直到在某一位的字符不相同或者已经到了最短的字符串的末尾字符,就结束运算。
public class Longest_Common_Prefix {
public String longestCommonPrefix(String[] strs) {
if(strs.length == 0) {
return "";
}
for(int i=0;i<strs[0].length();i++) {
char t = strs[0].charAt(i);
for(int j=1;j<strs.length;j++) {
if(i == strs[j].length() || strs[j].charAt(i) != t) {
return strs[0].substring(0, i);
}
}
}
return strs[0];
}
}
算法分析
时间复杂度:最坏情况下(所有字符串相同)O(S),一般情况下n*min(Si)
空间复杂度:O(1)
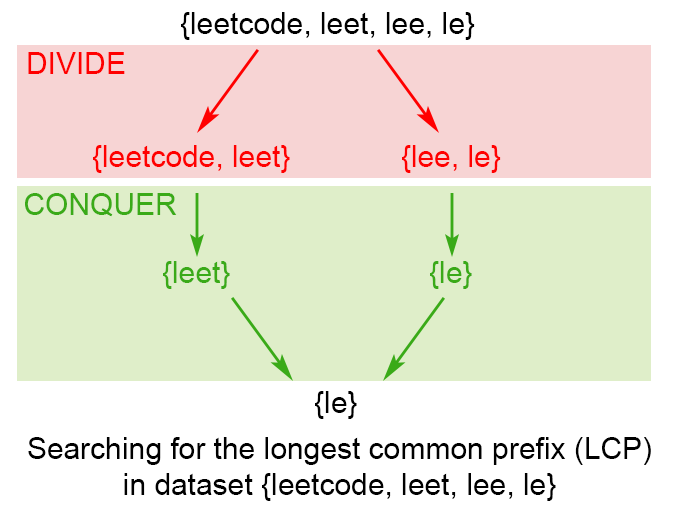
3. 方法三:分而治之
将字符数组分为两组,分别对两组查找最长公共前缀sl,sr,最后再计算sl和sr的公共前缀。
public class Longest_Common_Prefix {
//分而治之的方法
public String longestCommonPrefix(String[] strs) {
if(strs.length==0) {
return "";
}
return longestCommonPrefix(strs,0,strs.length-1);
}
private String longestCommonPrefix(String[] strs,int l,int r) {
if(l==r) {
return strs[l];
}
int mid = (l+r)/2;
String lcpLeft=longestCommonPrefix(strs,l,mid);
String lcpRight=longestCommonPrefix(strs,mid+1,r);
return commonPrefix(lcpLeft,lcpRight);
}
private String commonPrefix(String s1,String s2) {
int len=Math.min(s1.length(), s2.length());
for(int i=0;i<len;i++) {
if(s1.charAt(i) != s2.charAt(i)) {
return s1.substring(0, i);
}
}
return s1.substring(0,len);
}
}
算法分析
时间复杂度:最坏情况下为O(S),(S=mn,m为每个字符串的长度,n为字符串的个数)
空间复杂度:O(mlogn),算法logn次的递归调用,每次都需要m个存储空间
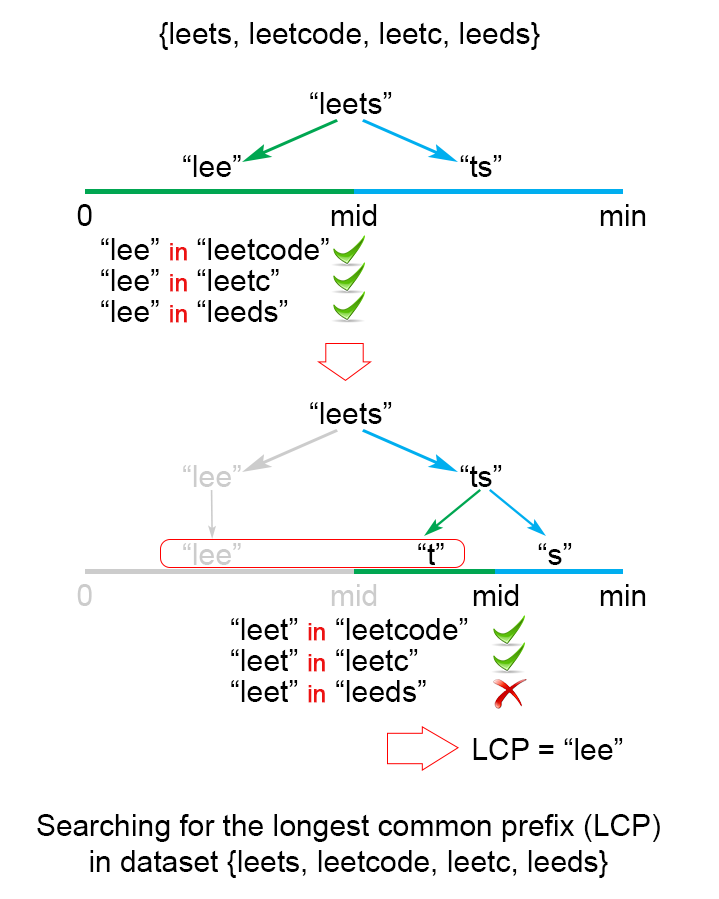
4. 方法四:二分法
首先找到字符串数组中最短字符串的长度minLen,它也是公共前缀的最大的长度,那么查找最长公共前缀的范围就缩小到每个字符串[0,minLen]之间。
将查找范围分为等长的两部分,[0,mid]和[mid+1,minLen],取第一个字符串的前半部分的子字符串substr1 = str1.subString(0,mid),去和其他的字符串比较判断substr1是不是公共前缀,这时会有两种情况:
如果substr1是公共前缀,那么就将substr1增加判断更长的子字符串是不是公共前缀
如果substr1不是公共前缀,那么对于长度大于substr1的字符串都不是公共前缀,这时减小substr1去判断更小的子字符串是不是公共前缀
class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0)
return "";
int minLen = Integer.MAX_VALUE;
for (String str : strs)
minLen = Math.min(minLen, str.length());
int low = 1;
int high = minLen;
while (low <= high) {
int middle = (low + high) / 2;
if (isCommonPrefix(strs, middle))
low = middle + 1;
else
high = middle - 1;
}
return strs[0].substring(0, (low + high) / 2);
}
private boolean isCommonPrefix(String[] strs, int len){
String str1 = strs[0].substring(0,len);
for (int i = 1; i < strs.length; i++)
if (!strs[i].startsWith(str1))
return false;
return true;
}
}
算法分析
时间复杂度:O(S * logn)
空间复杂度:O(1)
Valid Parentheses
Description
Given a string containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.
An input string is valid if:
1.Open brackets must be closed by the same type of brackets.
2.Open brackets must be closed in the correct order.
Note that an empty string is also considered valid.
Example
Example 1:
Input: "()"
Output: true
Example 2:
Input: "()[]{}"
Output: true
Example 3:
Input: "(]"
Output: false
Example 4:
Input: "([)]"
Output: false
Example 5:
Input: "{[]}"
Output: true
Solution
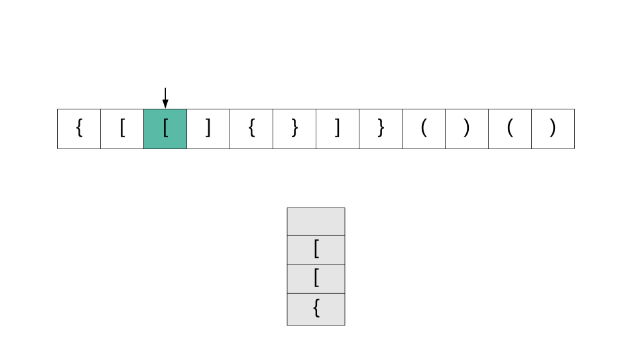
方法概述-堆栈法
对于一个有效的字符表达式,字符串中的括号都是成对出现的。正如题中所说,打开的括号必须有相同形式的关闭括号,并且所有打开的括号必须以正确的顺序关闭。
从起始位置开始检查字符串,如果第一个字符是关闭字符,那么这个字符串一定不是有效的;如果第一个是某种打开字符,将它压入堆栈 stack.push(char c),每遇到一个打开字符就做相同的操作;如果遍历字符串中遇到的关闭字符,看栈顶的字符是不是和此关闭字符相匹配的打开字符,如果是,将字符出栈并继续遍历,如果不是,那么就不是有效的字符串;顺利遍历完整个字符串时,检查栈是否为空,如果是空,那么字符串时有效的,否则无效。
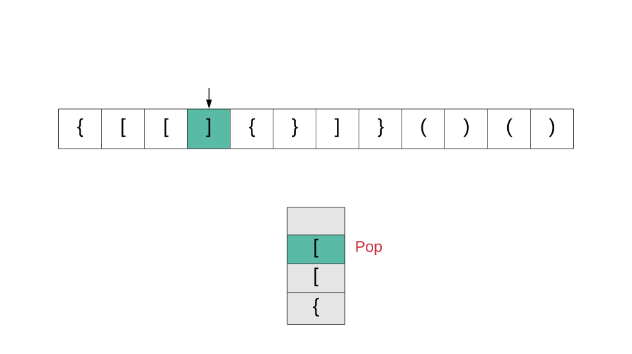
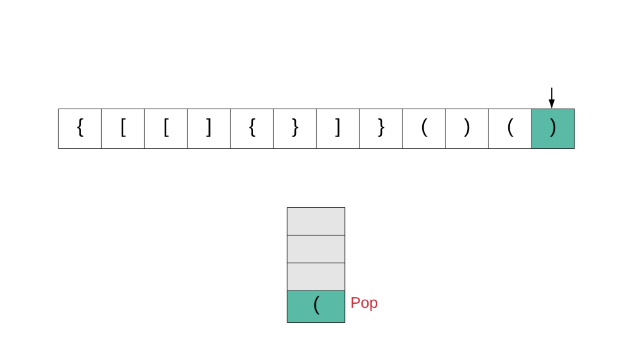
class Solution {
public boolean isValid(String s) {
if(s.isEmpty()) {
return true;
}
char[] stack = new char[s.length()];
int top = 0;
for(int i=0;i<s.length();i++) {
char c = s.charAt(i);
if(c=='{' || c=='[' || c=='(') {
stack[top++] = c;
}
if(c=='}') {
if(top==0 || stack[--top]!='{') {
return false;
}
}
if(c==']') {
if(top==0 || stack[--top]!='[') {
return false;
}
}
if(c==')') {
if(top==0 || stack[--top]!='(') {
return false;
}
}
}
return top==0;
}
}
Generate Parentheses
Description
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
Example
given n = 3, a solution set is:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
Solution
- 方法一:暴力法
方法概述:产生所有可能的字符串,检查每个字符串是不是有效形式。
public class Generate_Parentheses {
public List<String> generateParentheses(int n){
List<String> list = new ArrayList<String>();
generateAll(new char[2*n],0,list);
return list;
}
private void generateAll(char[] current,int index,List<String> result) {
if(index == current.length) {
if(valid(current)) {
result.add(new String(current));
}
}else {
current[index] = '(';
generateAll(current,index+1,result);
current[index] = ')';
generateAll(current,index+1,result);
}
}
private boolean valid(char[] current) {
int flag=0;
for(char c:current) {
if(c == '(') flag++;
else flag--;
if(flag<0) return false;
}
return (flag==0);
}
}
算法分析
时间复杂度:O(n*2^2n)
空间复杂度:O(n*2^2n)
- 方法二: 回溯算法
方法概述:回溯算法相当于穷举法(通用解法的美称),性能一般不太理想,但某些情况和穷举法相比性能也有显著的提升,和穷举法不同的是回溯法设置一些条件过滤了一些不可能的情况,回溯法一般用递归来解决
public class Generate_Parentheses {
//回溯法
public List<String> generateParentheses(int n){
List<String> list = new ArrayList<String>();
backtrack(list,"",0,0,n);
return list;
}
private void backtrack(List<String> list,String s,int open,int close,int max) {
if(s.length() == 2*max) {
list.add(s);
return;
}
if(open<max) {
backtrack(list,s+'(',open+1,close,max);
}
if(close<open) {
backtrack(list,s+')',open,close+1,max);
}
}
}
算法分析
时间复杂度:O(4^n/n^1/2)
空间复杂度:O(4^n/n^1/2)
Longest Valid Parentheses(32-Hard)
Description
Given a string containing just the characters ‘(‘ and ‘)’, find the length of the longest valid (well-formed) parentheses substring.
Example
Example 1:
Input: "(()"
Output: 2
Explanation: The longest valid parentheses substring is "()"
Example 2:
Input: ")()())"
Output: 4
Explanation: The longest valid parentheses substring is "()()"
Solution
- Approach 1. Dynamic Programming
public class Solution {
public int longestValidParentheses(String s) {
int maxans = 0;
int dp[] = new int[s.length()];
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == ')') {
if (s.charAt(i - 1) == '(') {
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
}
maxans = Math.max(maxans, dp[i]);
}
}
return maxans;
}
}
- Approach 2. Using Stack
public class Solution {
public int longestValidParentheses(String s) {
int maxans = 0;
Stack<Integer> stack = new Stack<>();
stack.push(-1);
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i);
} else {
stack.pop();
if (stack.empty()) {
stack.push(i);
} else {
maxans = Math.max(maxans, i - stack.peek());
}
}
}
return maxans;
}
}
- Approach 3. Without extra space
class Solution {
public int longestValidParentheses(String s) {
int left = 0, right = 0, maxlength = 0;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxlength = Math.max(maxlength, 2 * right);
}else if (right >= left) {
left = right = 0;
}
}
left = right = 0;
for (int i = s.length() - 1; i >= 0; i--) {
if (s.charAt(i) == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxlength = Math.max(maxlength, 2 * left);
} else if (left >= right) {
left = right = 0;
}
}
return maxlength;
}
}
Substring with Concatenation of All Words
Description
You are given a string, s, and a list of words, words, that are all of the same length. Find all starting indices of substring(s) in s that is a concatenation of each word in words exactly once and without any intervening characters.
Example
Input:
s = "barfoothefoobarman",
words = ["foo","bar"]
Output: [0,9]
Explanation: Substrings starting at index 0 and 9 are "barfoor" and "foobar" respectively.
The output order does not matter, returning [9,0] is fine too.
Solution Code
public class SubstringIndexOfAllWords {
public List<Integer> findSubString(String s, String[] words){
List<Integer> indexs = new ArrayList<Integer>();
int n = s.length();
int num = words.length;
if(n == 0 || num == 0)
return indexs;
int len = words[0].length();
//counts用于存储words中字符串的个数和每个字符串的个数
Map<String,Integer> counts = new HashMap();
for(String word : words) {
counts.put(word, counts.getOrDefault(word, 0) + 1);
}
for(int i = 0;i < n - num * len +1; i++) {
Map<String,Integer> temp = new HashMap();
int j = 0;
while(j < num) {
String word = s.substring(i + j * len, i + (j + 1) * len);
if(counts.containsKey(word)) {
temp.put(word, temp.getOrDefault(word, 0) + 1);
if(temp .get(word) > counts.get(word)) {
break;
}
}else {
break;
}
j++;
}
if(j == num) {
indexs.add(i);
}
}
return indexs;
}
}